Lead in to sine cosine or tangent – Lead in to sine, cosine, or tangent is a fundamental concept in trigonometry that plays a crucial role in calculating trigonometric ratios and understanding the relationship between angles and side lengths. This guide provides a comprehensive overview of lead in, its applications, geometric interpretation, computational techniques, and advanced applications, offering a thorough understanding of this essential trigonometric concept.

1. Definition and Introduction: Lead In To Sine Cosine Or Tangent

Lead in to sine cosine or tangentrefers to the process of converting an angle measure from degrees or radians to its corresponding sine, cosine, or tangent value using a reference angle.

This concept is crucial in trigonometry as it provides a systematic approach to determining trigonometric ratios for any given angle.

2. Applications in Trigonometry

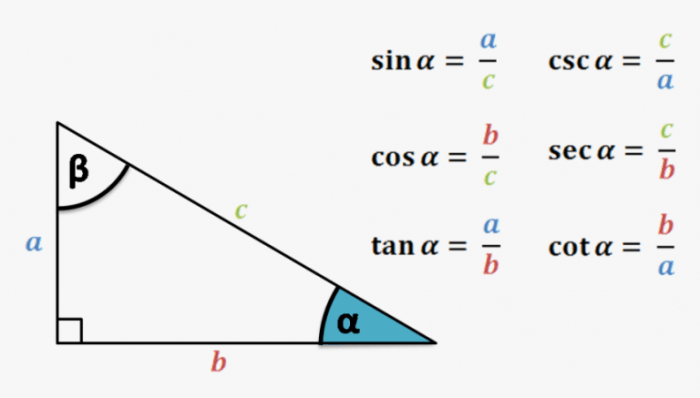
Calculating Trigonometric Ratios, Lead in to sine cosine or tangent

Lead in enables the calculation of sine, cosine, and tangent values for any angle by finding the corresponding reference angle and using the unit circle or trigonometric tables.

Relationship with the Unit Circle

The unit circle is a graphical representation of trigonometric functions where the lead in of an angle corresponds to the coordinates of a point on the circle.

3. Geometric Interpretation

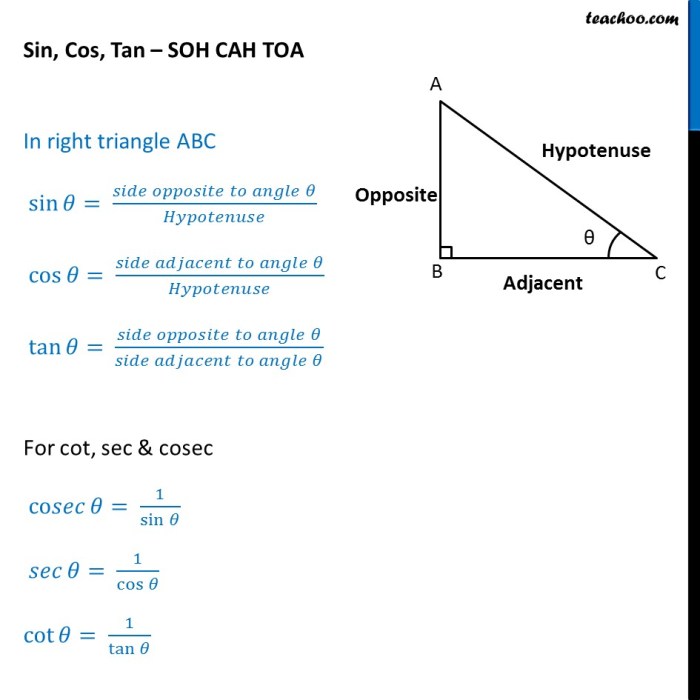
Right Triangle Interpretation

In a right triangle, the lead in of an acute angle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.

Finding Angles and Side Lengths

Lead in can be used to determine unknown angles or side lengths in right triangles using the Pythagorean theorem and trigonometric identities.

4. Computational Techniques

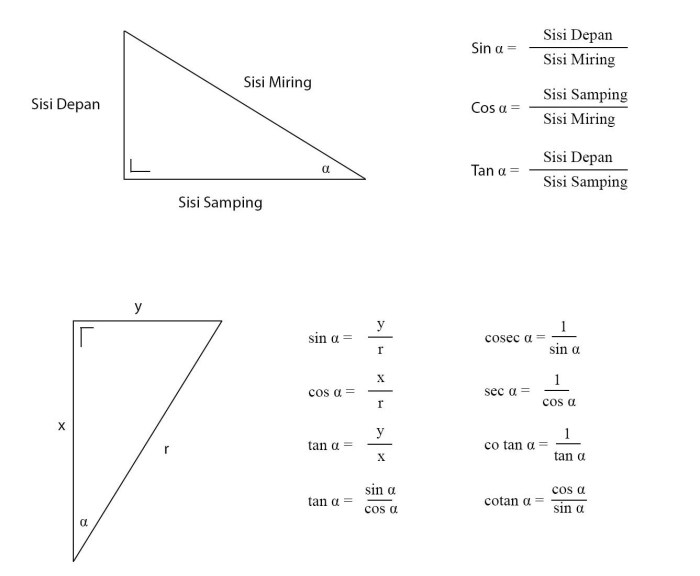
Using Calculators or Tables

Calculators and trigonometric tables provide direct methods for computing lead in for any given angle measure.

Step-by-Step Computation

To calculate lead in manually, one can use the following steps:

1. Convert the angle measure to radians if necessary.
2. Find the coterminal angle within the range [0, 2π).
3. Use the unit circle or trigonometric identities to determine the corresponding sine, cosine, or tangent value.

5. Advanced Applications

Calculus

Lead in plays a role in calculus, particularly in the study of derivatives and integrals of trigonometric functions.

Physics

In physics, lead in is used in applications involving circular motion, projectile motion, and wave phenomena.

Quick FAQs

What is the significance of lead in in trigonometry?

Lead in is crucial in trigonometry as it allows for the calculation of trigonometric ratios (sine, cosine, and tangent) for any given angle, enabling the analysis of relationships between angles and side lengths in triangles.

How is lead in used to find angles and side lengths?

Using the geometric interpretation of lead in in a right triangle, one can establish relationships between the angle, opposite side, and adjacent side, allowing for the determination of unknown angles or side lengths through trigonometric ratios.