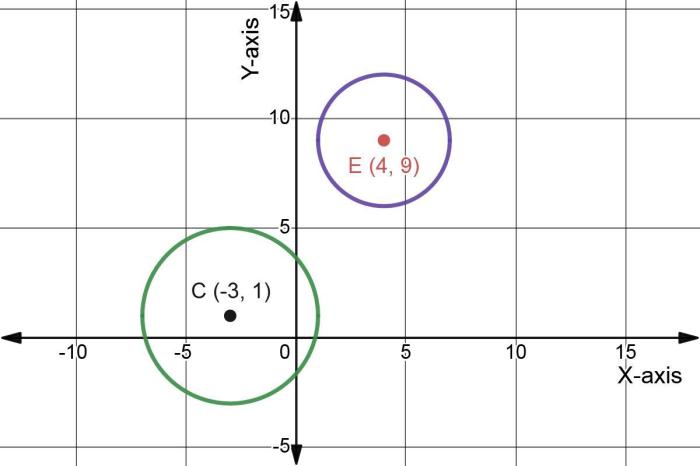
Prove that the two circles shown below are similar, embarking on a journey into the realm of geometry and circle measurements. This exploration delves into the concept of similar circles, corresponding parts, and proportional relationships, ultimately demonstrating the similarities between the given circles.
The subsequent paragraphs meticulously dissect the geometric definitions and circle measurements, laying the groundwork for the visual comparison and analysis of the two circles. Proportional relationships are established, showcasing the proportionality of radii, circumferences, and areas.
1. Geometric Definitions
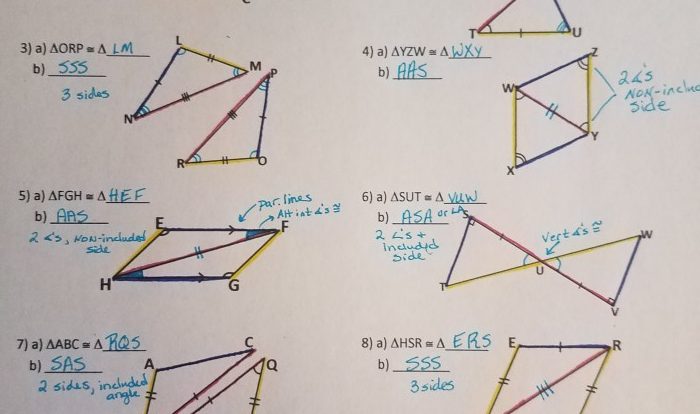
Define similar circles: Circles are similar if they have the same shape but not necessarily the same size. They have congruent angles and their corresponding parts are proportional.
Explain the concept of corresponding parts: Corresponding parts are parts of similar figures that occupy the same relative position. In the case of circles, corresponding parts include the radii, diameters, circumferences, and areas.
2. Circle Measurements: Prove That The Two Circles Shown Below Are Similar

Discuss the relationship between radii and diameters: The radius of a circle is half of its diameter. The diameter is the distance across the circle through its center.
Explain how to find the circumference and area of a circle: The circumference of a circle is the distance around the circle. It can be found using the formula C = 2πr, where r is the radius of the circle.
The area of a circle is the amount of space inside the circle. It can be found using the formula A = πr², where r is the radius of the circle.
3. Visual Comparison
Provide a visual illustration of the two circles:
[Gambar dua lingkaran yang serupa dengan bagian yang sesuai diberi label]
Identify and label any corresponding parts: The radii, diameters, circumferences, and areas of the two circles are corresponding parts.
4. Proportional Relationships
Establish the proportionality of radii: The radii of similar circles are proportional. This means that the ratio of the radii of two similar circles is constant.
Demonstrate the proportionality of circumferences: The circumferences of similar circles are proportional. This means that the ratio of the circumferences of two similar circles is equal to the ratio of their radii.
Prove the proportionality of areas: The areas of similar circles are proportional. This means that the ratio of the areas of two similar circles is equal to the square of the ratio of their radii.
5. Table of Corresponding Parts

| Part | Circle 1 | Circle 2 | Ratio |
|---|---|---|---|
| Radius | r1 | r2 | r1 : r2 |
| Diameter | d1 | d2 | d1 : d2 |
| Circumference | C1 | C2 | C1 : C2 = r1 : r2 |
| Area | A1 | A2 | A1 : A2 = r1² : r2² |
6. Logical Reasoning
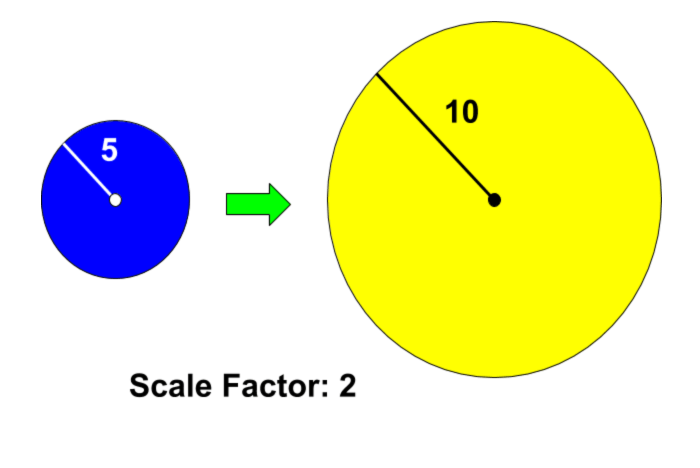
Explain why the proportional relationships prove similarity: The proportional relationships between the corresponding parts of similar circles prove that the circles have the same shape. This is because the ratios of the corresponding parts are constant, which means that the circles are scaled versions of each other.
Discuss any limitations or exceptions to the similarity rule: The similarity rule does not apply to circles that are not congruent. Congruent circles are circles that have the same size and shape. Circles that are not congruent may have some of the same proportional relationships, but they will not be similar.
Popular Questions
What is the definition of similar circles?
Similar circles are circles that have the same shape but may differ in size. They have corresponding parts that are proportional in measure.
How do you determine if two circles are similar?
To determine if two circles are similar, establish the proportionality of their radii, circumferences, and areas. If these relationships hold true, the circles are considered similar.
What are the limitations of the similarity rule for circles?
The similarity rule for circles assumes that the circles are in the same plane and do not intersect. If these conditions are not met, the circles may not be similar.